Home Estruturas Diagrama de Momento Fletor

Estruturas

Diagrama de Momento Fletor

Nelso Schneider

26/07/2019

O diagrama de momento fletor é uma representação visual, baseada em modelos matemáticos, das forças de momento que atuam em uma estrutura. Mas vamos começar do princípio:

O momento é definido como uma uma “força aplicada em um sistema rotacional a uma determinada distância do eixo de rotação”:

Imagine que você está dirigindo seu carro e, por um acaso, um dos seus pneus fura, você desce e pega a chave no porta malas para afrouxar os parafusos que prendem a roda, você encaixa a chave no primeiro parafuso e faz força, mas o parafuso está apertado demais e não se mexe.

É intuitivo imaginar que, se você usar uma chave mais longa, ou algo que alongue a haste da chave, formando um “braço de alavanca” maior, será mais fácil afrouxar o parafuso.

O momento é justamente essa relação entre a força e a distância do eixo em que aplicamos essa força, de forma que, quanto mais longe do eixo, menos força precisa ser aplicada para que um mesmo momento seja gerado.

Indicamos que você leia nosso artigo sobre Diagrama de Esforço Cortante, pois utilizaremos aqui vários conceitos que foram apresentados lá, além de darmos continuidade ao mesmo exemplo.

Artigo: Diagrama de Esforço Cortante

Integral:

Para fazermos um diagrama de momento fletor temos que seguir o mesmo princípio de integração apresentado no artigo Diagrama de Esforço Cortante, no entanto temos que integrar o diagrama de esforço cortante dessa vez:

Cargas pontuais passam a ser funções constantes que, por sua vez, passam a ser funções de primeiro grau (ax+b):

Cargas distribuídas (constantes) passa a ser funções de primeiro grau (ax+b) que, por sua vez passam a ser funções de segundo grau (ax²+bx+c):

*Perceba que o ponto em que o momento atinge seu máximo é o mesmo ponto em que a reta do esforço cortante cruza o eixo X.

Cargas descritas por uma função de primeiro grau passam a ser funções de segundo grau (ax²+bx+c) que, por sua vez passam a ser funções de terceiro grau (ax³+bx²+cx+d):

*Perceba que o ponto em que o momento atinge seu máximo é o mesmo ponto em que a curva do esforço cortante cruza o eixo X.

Exemplo 1 – Cargas Concentradas:

Primeiro utilizamos a equação de equilíbrio dos momentos para encontrar a força das reações dos apoios RA e RB:

Prova real:

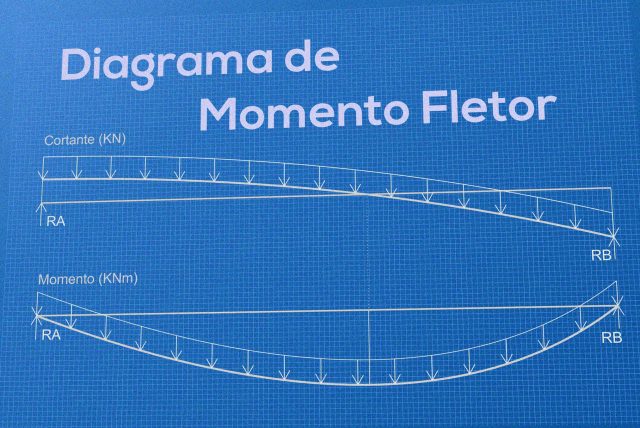
Com as reações dos apoios descobertas, podemos traçar o diagrama de esforço cortante:

Teoria:

Integrando cada trecho

A constante 6,3275 passa a ser a expressão 6,3275*X

A constante 0,1275 passa a ser a expressão 0,1275*X

A constante -8,3725 passa a ser a expressão -8,3725*X

Multiplicando por X, temos os seguintes resultados:

6,3275*1,7 = 10,75675 KNm

0,1275*1,0 = 0,1275 KNm

-8,3725*1,3 = 10,88425 KNm

Com esses resultados podemos desenhar nosso diagrama de momento fletor:

*O diagrama de momento fletor é feito com os valores positivos no lado de baixo e os valores negativos no lado de cima (convenção), pois dessa forma o desenho representa as posições das armaduras que serão colocadas em uma viga.

Prática:

A área de cada trecho do diagrama de esforço cortante equivale à variação do mesmo trecho no diagrama de momento fletor, como na imagem:

Onde a área do retângulo vermelho de 6,3275 KN * 1,7 m = 10,75675 KNm e o retângulo azul de 8,3725 KN * 1,3 m = 10,88425 KNm.

É importante ter em mente também que o ponto onde o diagrama de esforço cortante cruza o eixo X é sempre o ponto onde o momento atinge o máximo.

Exemplo 2 – Cargas distribuídas:

Primeiro fazemos a simplificação das cargas para poder utilizar a equação do equilíbrio dos momentos:

Sabendo que a força resultante de 32,0 KN está localizada no centro da estrutura, podemos então utilizar a equação do equilíbrio dos momentos:

Com as reações dos apoios descobertas, podemos traçar o diagrama de esforço cortante:

Teoria:

O carregamento forma uma função constante de 8,0. Para fazermos o diagrama de esforço cortante, integramos essa função constante:

Detalhe: Sabemos que o diagrama de esforço cortante inicia (no lado esquerdo) acima do eixo X, essa distância é exatamente a reação RA (quando a extremidade da viga for apoiada). Caso a extremidade da viga seja em balanço, o diagrama de esforço cortante inicia em zero.

Essa distância vertical entre o eixo X e o ponto onde a nossa reta inicia é prevista matematicamente como o “+b” da equação de primeiro grau (aX+b):

8,0 passa a ser -8X+16.

Essa equação será negativa em função da direção em que esta carga está sendo aplicada, já que sabemos que a reta percorrerá uma direção decrescente.

Com a equação do esforço cortante, fazemos então mais uma integral para obter a equação que descreve o momento fletor:

-8X+16 passa a ser -4X²+16X

Para calcularmos o momento máximo, em teoria, temos que fazer a derivada da equação (-4X²+16X) e igualarmos a zero, dessa forma estamos calculando qual a posição em que a inclinação da reta é nula, em uma parábola isso só acontece em um único ponto.

Sabemos então que o ponto onde o momento atinge seu máximo é em X=2, usamos essa informação na equação principal:

Podemos ainda conferir se nas extremidades da viga o momento será nulo, onde X=0 (início da viga) e X=4 (final da viga):

Com todas essas informações, podemos então desenhar o diagrama:

Prática:

Sabendo o formato que o diagrama deve ter, podemos simplesmente calcular a área de um dos triângulos formados no diagrama de esforço cortante para sabermos o momento máximo. Lembrando que o momento máximo fica localizado onde o diagrama de esforço cortante cruza o eixo X.

Sabendo também que o momento é nulo nos apoios, já temos as informações necessárias para desenhar nosso diagrama de momento fletor exatamente como na imagem anterior.

Exemplo 3 – Carga triangular:

Primeiro fazemos a simplificação das cargas para poder utilizar a equação do equilíbrio dos momentos:

Sabemos que a força resultante se localiza a 2/3 do início da viga:

Equação de equilíbrio dos momentos:

Com as reações dos apoios descobertas, podemos traçar o diagrama de esforço cortante:

Teoria:

Infelizmente para esse tipo de carregamento não temos uma forma prática.

Sabemos que o carregamento atinge um pico de 7,5 KN depois de percorrer 4,0 m, então podemos deduzir que , ou seja, a cada 1,0 m percorrido, a carga aumenta 1,875 KN.

Podemos deduzir então que o carregamento segue a equação:

Para obtermos o diagrama de esforço cortante, fazemos a integral dessa equação, lembrando que a curva deve começar 4,9875 acima do eixo X, ou seja, fazemos a integral da equação primária (1,875X) e adicionamos “+4,9875” ao final dela. Outro detalhe é que temos que inverter o sinal da equação para que o desenho fique correto.

Com a equação do esforço cortante, fazemos então mais uma integral para obter a equação que descreve o momento fletor.

Agora que temos a equação que descreve o momento fletor, falta apenas achar o momento máximo:

Momento máximo em carregamentos triangulares:

Primeiro precisamos achar a posição em que o diagrama de esforço cortante cruza o eixo X, para isso, igualamos a equação do esforço cortante a zero e utilizamos a fórmula de Bhaskara:

O termo “a” da equação de Bhaskara é -1,875/2, que podemos colocar como -0,9375;

O termo “b” é inexistente, portanto, zero, e;

O termo “c” é 4,9875.

Utilizaremos o valor positivo (X”).

Agora que sabemos o ponto onde o diagrama de esforço cortante cruza o eixo X, podemos calcular a área indicada:

Para calcularmos a área indicada vamos precisar usar a integral definida.

A integral definida vai ter os limites de 0 a 2,3065:

Indicamos o uso do Integral Calculator para o cálculo de integrais. Basta escrever sua equação na caixa de texto. Para impor os limites você deve clicar em “options” no lado direito da caixa de texto.

Sabemos então que o ponto onde o momento atinge o seu máximo fica em X = 2,3065 m e equivale a 7,67 KNm:

Lembrando que o diagrama de momento fletor tem seus lados positivo e negativo invertidos.

Exemplo 4 – Continuação do exercício do artigo anterior (Diagrama de Esforço Cortante:

Vamos separar o diagrama de esforço cortante em trechos, para facilitar os cálculos:

Trecho 1:

O trecho 1 é dado por uma função constante de 13,5, integrando uma vez, obtemos a função de 13,5X.

Trecho 2:

O trecho 2 é dado por uma função constante de 6,3, integrando uma vez, obtemos a função de 6,3X, mas devemos ainda somar a altura resultante do primeiro trecho, onde 13,5*1,0 m = 13,5, temos assim a função 6,3X+13,5.

Trecho 3:

O trecho 3 é dado uma uma função de primeiro grau: 4,2X, integrando uma vez obtemos a função 2,1X², no entanto, essa função vai precisar de algumas informações adicionais:

Primeiro: Temos que inverter o sinal da primeira parte da equação: -2,1X²

Segundo: Temos que adicionar o “b” da equação, que será dado em função da equação anterior: 6,3X. Então temos até agora a seguinte equação: -2,1X²+6,3X. Desta forma temos a parábola e a posição X em que ela se localiza, falta apenas a altura dela:

Terceiro: Temos que adicionar o “c” da equação, que é dado em função da altura atingida pela soma dos 2 trechos anteriores, ou seja:

13,5*1,0 m = 13,5 KNm

6,3*1,0 m + 13,5 = 19,8 KNm

Finalmente obtemos a equação: -2,1X²+6,3X+19,8

Sabemos também que o diagrama de esforço cortante cruza o eixo X a 3,5 m do começo da viga (lado direito). Para saber quanto é o momento máximo basta calcularmos a área do triângulo formado no trecho 3 e somarmos com os 19,8 (área dos outros 2 trechos):

(6,3*1,5)/2 = 4,725 + 19,8 = 24,525 KNm

Trecho 4:

É a continuação do trecho 3, porém devemos mudar as coordenadas da equação em função da carga concentrada e do novo ponto de início:

Mantemos o -2,1X² por se tratar ainda de uma função de segundo grau;

trocamos o 6,3X (era a altura do ponto onde a equação começava, entre o trecho 3 e o trecho 2) por 6,5X (em relação a carga concentrada);

A altura do ponto de início que antes era 19,8 passa a ser 24,525, já que o ponto de início desse trecho coincide com o ponto de momento máximo que calculamos anteriormente.

Obtemos então:

Trecho 5:

A equação que descreve o diagrama de esforço cortante no trecho 5 é dada por:

Fazemos então a integral dela:

Porém ainda temos que adicionar a variação de altura dela (+c). Para descobrirmos esse valor basta resolvermos a equação do trecho 4 com x=0,5m:

Nossa equação do trecho 5 fica assim:

Como sabemos que, ao final da viga o momento tem que ser zero, já que sua extremidade está apoiada, podemos fazer uma prova real deste último trecho. Substituindo X por 2 m na equação, o resultado deve ser zero: