Neste artigos vamos desenvolver o entendimento de Viga Gerber através de um exercício resolvido e passo a passo. Mas antes, vamos entender um pouco da sua aplicabilidade.
Para falar sobre Vigas Gerber precisamos voltar a 1968, quando as obras da ponte Rio-Niterói foram iniciadas com o objetivo de facilitar a vida dos cidadãos cariocas.
Essa construção reduziria para 13 Km um trajeto que até então era de mais de 100 Km, já que os cidadãos tinham que dar a volta na Bahia de Guanabara para acessar o município vizinho.
Como nem tudo são flores, os projetistas tinham na mão um grande problema: A ponte não podia atrapalhar o tráfego dos grandes barcos que precisavam acessar a Bahia de Guanabara.
A solução?
Uma viga Gerber formando o maior vão livre com viga reta do mundo, com 300 metros de extensão e 72 metros de altura.
Ao todo são três vigas Gerber: uma metálica no centro e uma de concreto em cada lado.
Olha só:
Mas vamos começar do princípio:
Viga Gerber é definida como um conjunto de vigas que podem ou não ter estabilidade própria, mas a associação delas forma um conjunto perfeitamente estável.
Imagine a seguinte situação:
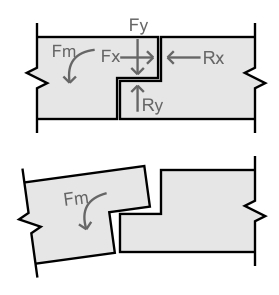
O trecho 01 não tem estabilidade própria e se unirmos ele com o trecho 02 utilizando um engaste, teremos uma viga hiperestática, mas se unirmos ele com o trecho 02 utilizando uma rótula, teremos uma viga Gerber:
Uma rótula é uma ligação entre vigas, ou seja, um encaixe, que transmite forças verticais e horizontais, mas não transmite momento, é justamente isso que faz com que a junção dos trechos não se transforme em uma única viga hiperestática.
Exercício 01 – Viga Gerber:
Vamos tomar como exemplo a seguinte situação: Uma primeira viga, com apenas um apoio real (RA) se apoia em outra viga, de forma que o conjunto deverá estar em equilíbrio:
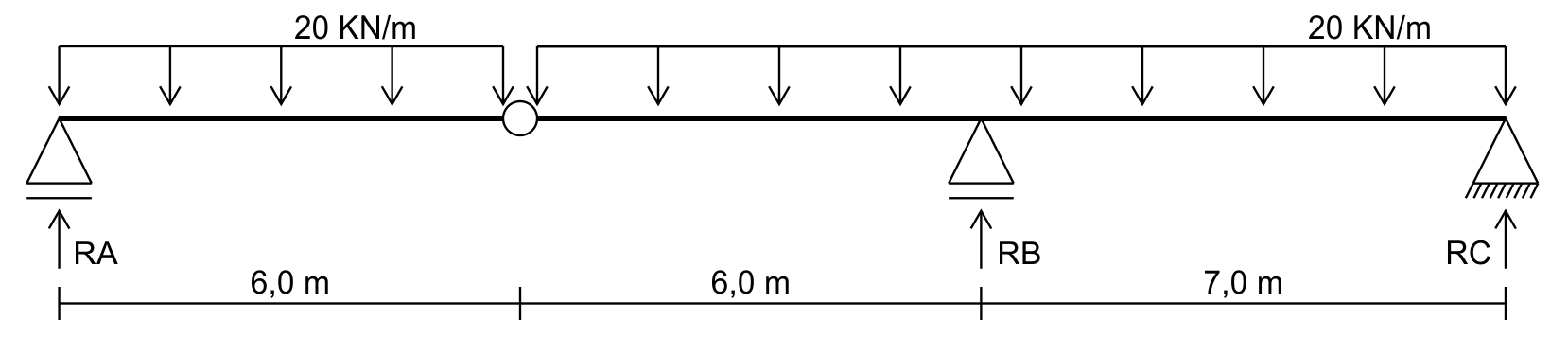
Temos que descobrir as reações RA, RB e RC porém, há um detalhe importante que deve ser levado em consideração:
- Temos que começar sempre pelo trecho com menos incógnitas (reações desconhecidas), já que as incógnitas podem se acumular durante o processo de resolução das equações.
No primeiro trecho temos apenas uma incógnita: a reação RA, enquanto no segundo trecho temos duas: RB e RC, portanto, vamos começar pelo primeiro:
Primeiro temos que separar esse trecho do resto da viga e, para isso vamos colocar um apoio virtual no local onde fica a rótula.
Esse apoio virtual é apenas um artifício para conseguirmos calcular o percentual de peso que será transferido para o segundo trecho.
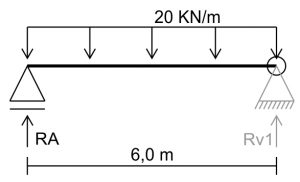
Chamaremos esse apoio de Reação Virtual 1 (Rv1) e, como o apoio RA é um apoio de primeiro gênero, nosso apoio virtual deverá ser de segundo gênero para que esse trecho esteja em equilíbrio.
Agora podemos calcular o valor da Reação RA e carga que será apoiada no segundo trecho, que chamamos de Rv1, por meio da equação de equilíbrio dos momentos:
Para descobrirmos a reação Rv1 vamos partir do ponto RA:
Para descobrirmos a reação RA vamos partir do ponto Rv1:
Agora temos as duas reações descobertas:
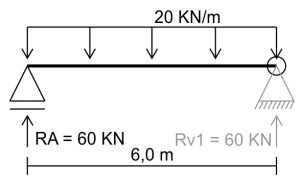
Com isso sabemos que 60 KN serão descarregados no apoio RA e os outros 60 KN serão descarregados como uma carga concentrada no início do segundo trecho.
Agora podemos calcular o segundo trecho:
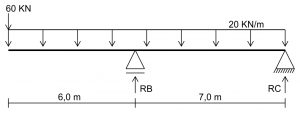
Como o segundo trecho da nossa Viga Gerber já é isostático, ao invés de usarmos um apoio virtual, vamos considerar como sendo um trecho em balanço com uma carga concentrada na ponta:
A carga de 60 KN que era descarregada no apoio Rv1 passa para o segundo trecho como uma carga concentrada, no mesmo ponto onde há a rótula.
Podemos então calcular os valores das reações RB e RC:
Para calcularmos a reação RC vamos partir do ponto RB:
Como o resultado foi negativo, podemos entender que a viga faz força para cima, transferindo para o apoio um esforço de tração, ao contrário do que estamos acostumados.
Para calcularmos o valor de RB vamos partir do ponto RC:
Podemos ainda utilizar a equação do equilíbrio dos esforços verticais para conferir se os cálculos estão corretos:
Se o somatório das forças verticais for igual a zero, significa que a nossa viga está estável.
Com todas as reações calculadas, podemos desenhar o diagrama de corpo livre e o diagrama de esforço cortante:
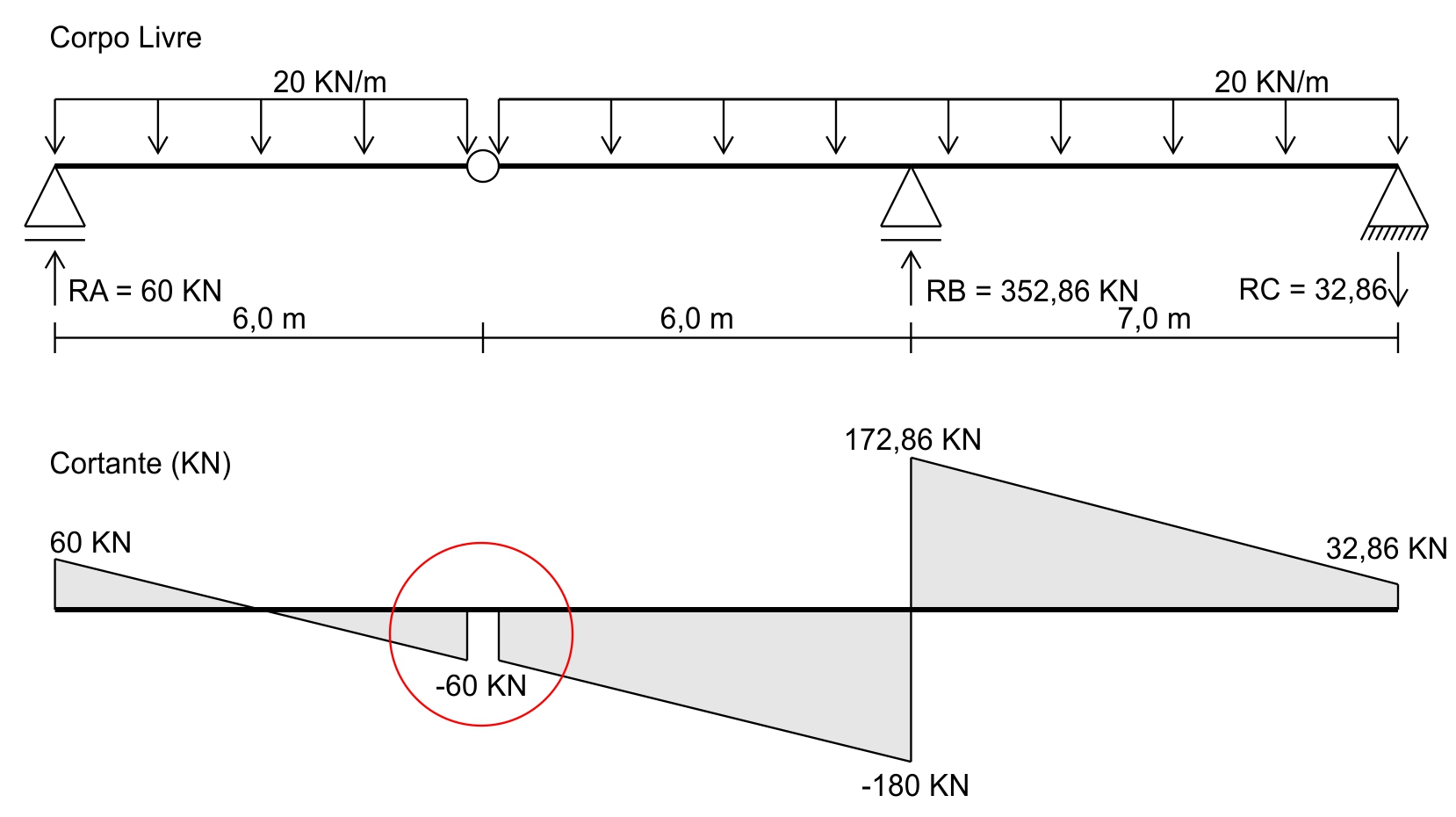
Na área circulada podemos considerar que a linha sobe em função da reação virtual e imediatamente depois desce em função da carga concentrada (lembrando que espaço entre as retas dentro do círculo é meramente ilustrativo).
- Se você tiver qualquer dúvida em relação ao diagrama de esforço cortante ou à utilização da equação de equilíbrio do momento fletor, você pode conferir o nosso artigo: Diagrama de Esforço Cortante.
Com o diagrama de esforço cortante da nossa Viga Gerber desenhado, podemos então desenhar o diagrama de momento fletor:
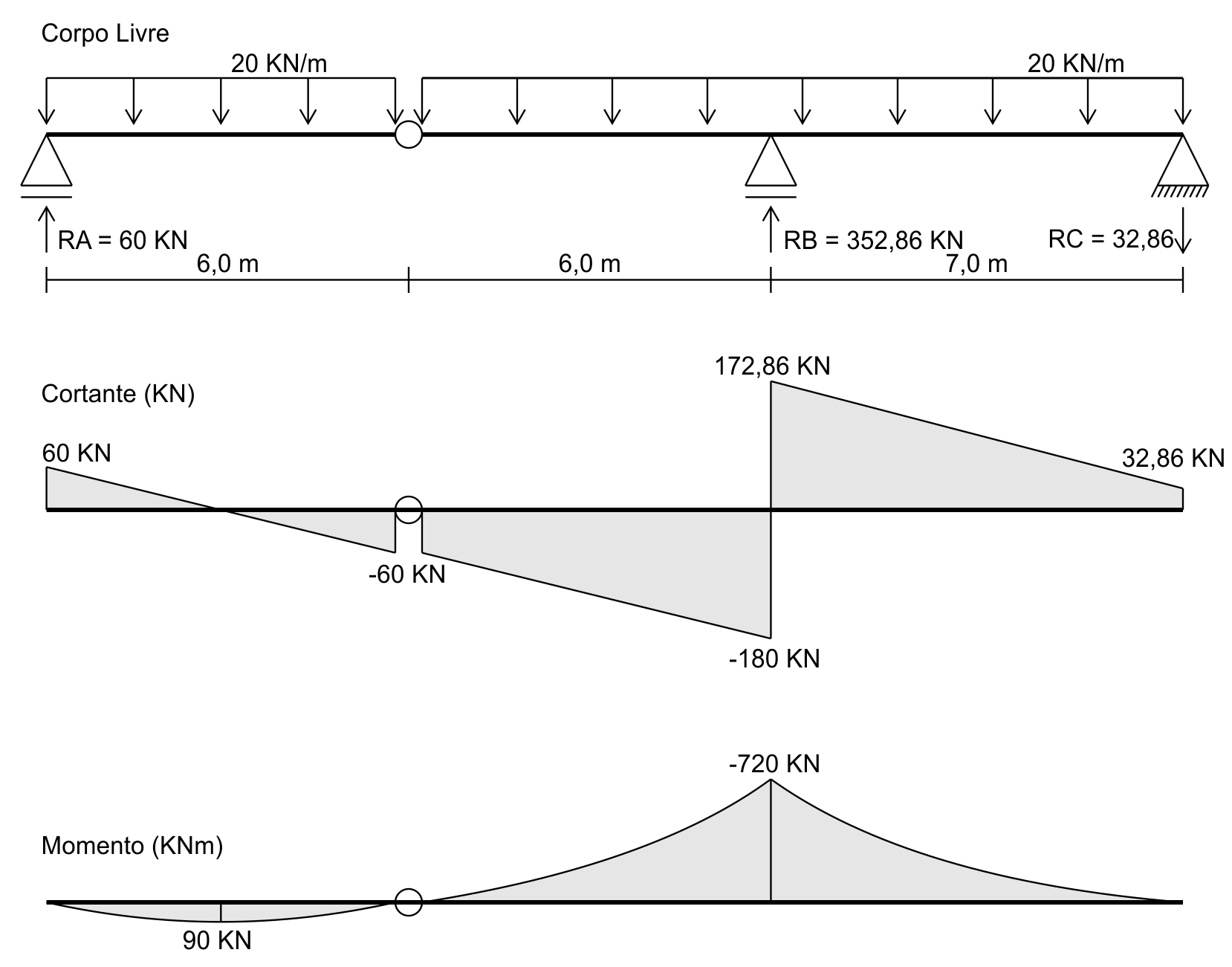
- Se você tiver qualquer dúvida em relação ao diagrama de momento fletor, você pode conferir o nosso artigo: Diagrama de Momento Fletor.
Exercício 2:
Para o segundo exercício vamos considerar uma estrutura um pouco mais parecida com a ponte Rio-Niterói:
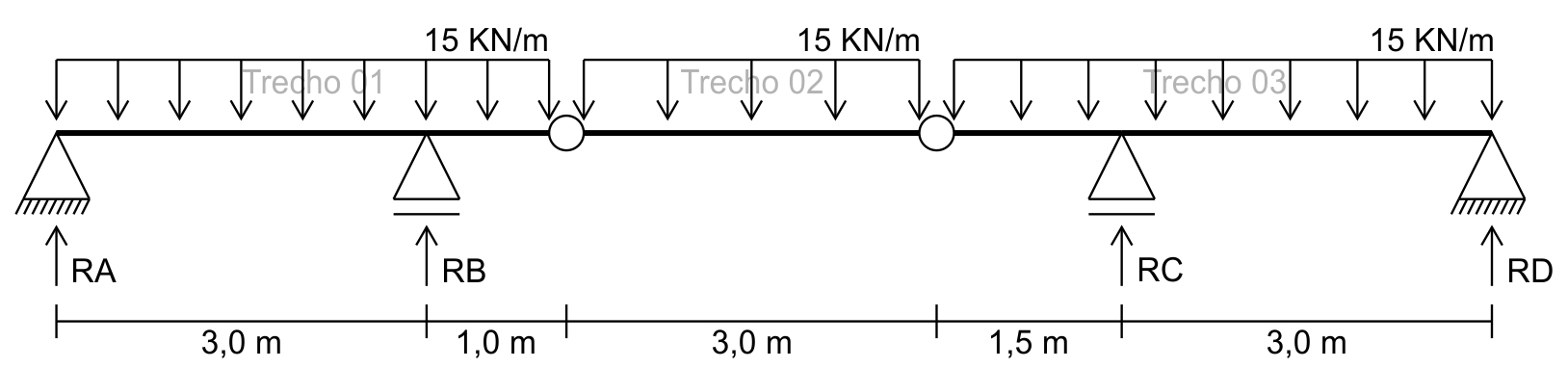
Primeiro temos que descobrir as reações RA, RB, RC e RD e, como comentado no exercício anterior, temos que começar pelo trecho com menos incógnitas, nesse caso, será o trecho 02, entre as rótulas.
Vamos imaginar esse trecho isolado como tendo dois apoios, um de segundo gênero e um de primeiro gênero, para podermos calcular a força que esse trecho aplicará nos outros dois:
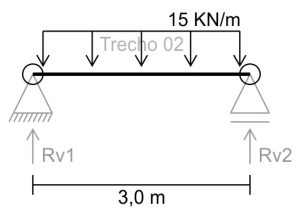
Para calcularmos a reação Rv2 vamos partir do ponto Rv1:
Para calcularmos a reação Rv1 vamos partir do ponto Rv2:
Sabemos então que, na primeira rótula teremos uma carga concentrada (no trecho 01) de 22,5 KN e na segunda rótula teremos uma carga concentrada (no trecho 03) de 22,5 KN.
Podemos seguir em frente no dimensionamento e agora calcular um dos trechos restantes, mas vamos começar pelo trecho 01.
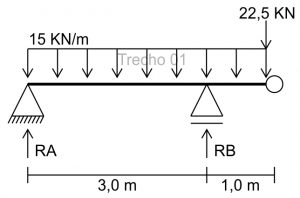
Para calcularmos a reação RB vamos partir do ponto RA:
Para calcularmos a reação RA vamos partir do ponto RB:
Agora vamos para o trecho 03:
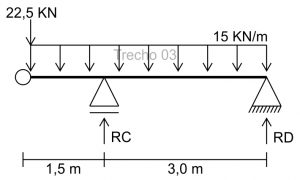
Para calcularmos a reação RD vamos partir do ponto RC:
Para calcularmos a reação RC vamos partir do ponto RD:
Agora que já não temos mais incógnitas, podemos desenhar o diagrama de corpo livre e o diagrama de esforço cortante:
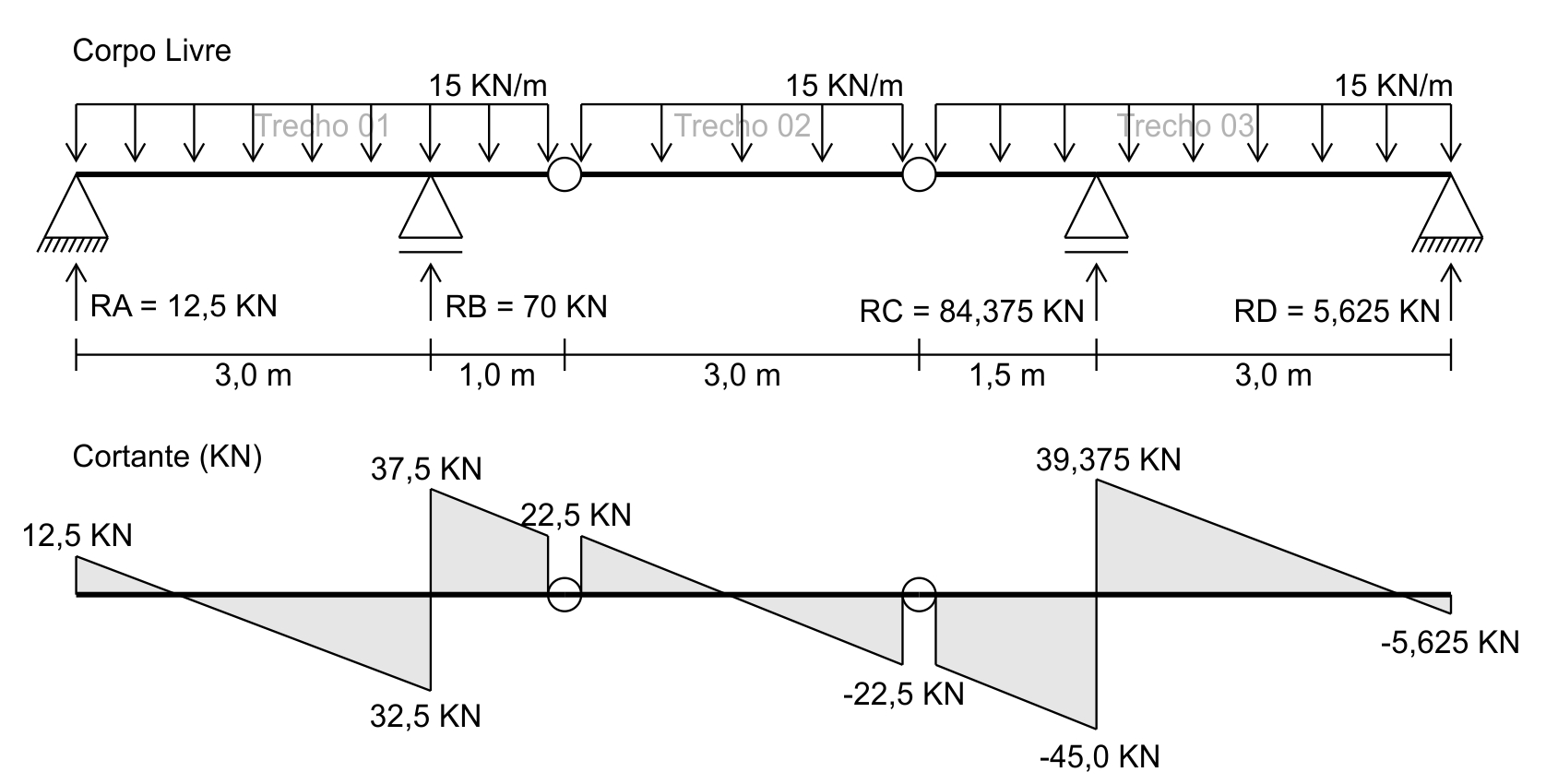
Com o diagrama de esforço cortante podemos então desenhar o diagrama de momento fletor:
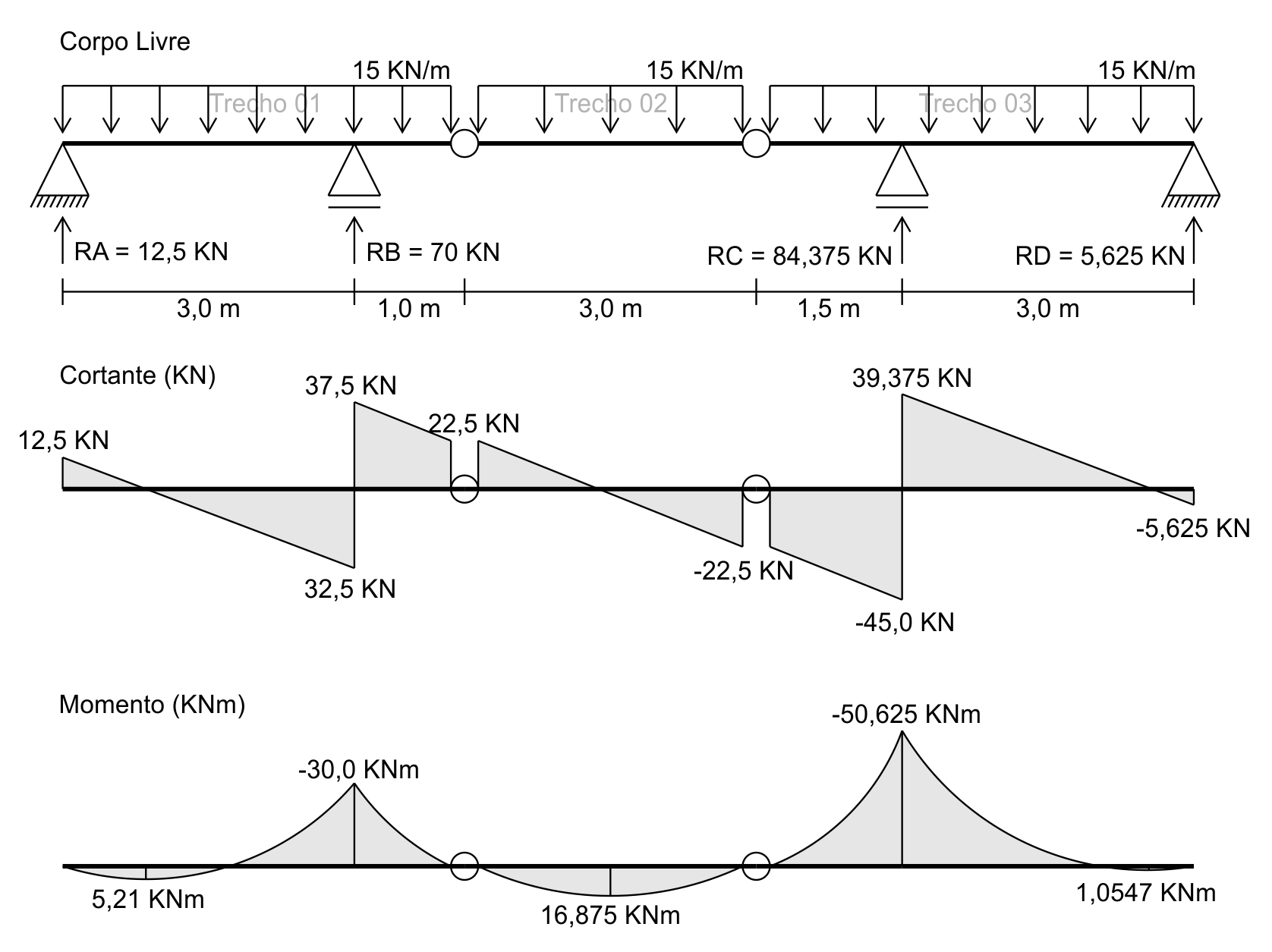
Espero que este artigo sobre Viga Gerber possa ter ajudado.
Se você gosta do tema de dimensionamento de vigas, tenho certeza que vai adorar um vídeo que eu realizei em meu canal do YouTube.
Nele eu dimensionei uma viga biapoiada de forma completa, incluindo as armaduras longitudinais.
Para acessar, é só clicar no link abaixo:
Se você gostou do artigo deixa um comentário e um like aqui em baixo para ajudar a divulgar o nosso blog.
Até uma próxima, abraço!
Gostaria de receber em pdf no meu e-mail esse assunto de vigas veber
Show muito bem explicado com detalhes facilita bastante o entendimento, parabéns
onde encontro o material relacionado a essas vigas gênero?