O cisalhamento em vigas é originário dos esforços cortantes, que são provenientes dos carregamentos exercidos sobre elas. Geralmente no dimensionamento de vigas de concreto armado no estado limite último (ELU), as primeiras armaduras calculadas são as de flexão (longitudinais), e em seguida são determinadas as armaduras ao cisalhamento (transversais).
O estudo e avaliação quanto ao cisalhamento, é um fator de grande relevância para dimensionamentos e projetos estruturais de vigas de concreto armado. Isso principalmente pela característica de heterogeneidade do material (concreto), o que acarreta um comportamento diferente quanto ao cisalhamento em relação a outros materiais, fugindo um pouco dos princípios comuns.
Atualmente no Brasil e nas principais referencias normativas do mundo, o modelo mais utilizado para cálculo de vigas a flexão simples é chamado de “Modelo de Treliça”. A partir desse modelo a ABNT NBR 6118:2014 – Projeto de estruturas de concreto – Procedimento – aponta dois modelos de cálculo que podem ser utilizados para dimensionamento de vigas ao cisalhamento.
Para entender como funciona a analogia das treliças em vigas de concreto armado, quais são e como funcionam os modelos de dimensionamento de vigas a cortante apresentados pela norma, além de acompanhar um exercício prático de cálculo de armaduras transversais (estribos) de uma viga, leia este artigo até o final!
Modelo de Treliças – Comportamento de vigas ao cisalhamento
O modelo clássico de treliça já citado anteriormente foi criado por Ritter e Mörsh, ainda no início do século XX. Este modelo se baseia no estudo do comportamento de uma viga com fissuras inclinadas no estádio II em analogia a uma treliça isostática, onde as forças nas barras podem ser determinadas considerando as condições de equilíbrio nos nós, a partir do esforço cortante.
Apesar de existirem divergências em resultados de ensaios, o modelo clássico de treliças considera que as fissuras (bielas de compressão) tenham inclinação de 45º e os banzos sejam paralelos entre si, considera ainda uma treliça isostática, configurando o não engasgamento dos nós (ligações banzos-bielas), além disso, o modelo pressupõe a armadura de cisalhamento com inclinação entre 45º e 90º.
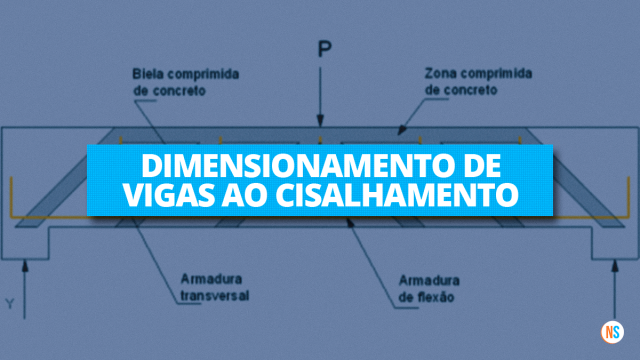
Com isso, a treliça formada pela analogia de uma viga bi-apoiada de seção retangular após a fissuração é composta pelo banzo superior (cordão de concreto comprimido), banzo inferior (armadura longitudinal de tração), diagonais comprimidas (bielas de concreto entre as fissuras) e as diagonais tracionadas (armaduras transversais de cisalhamento).
A partir disso a ABNT NBR 6118:2014 no item 17.4.1, pressupõe que o dimensionamento de elementos lineares à força cortante pode ser realizado através de dois modelos de calculo, o Modelo de cálculo I e o Modelo de cálculo II. Ambos consideram a analogia do modelo de treliça, de banzos paralelos, associado a mecanismos resistentes complementares desenvolvidos no interior da peça e traduzidos por uma componente adicional (Vc). Nos próximos tópicos do artigo nos aprofundaremos em cada um dos modelos propostos pela norma.
Verificação do ELU – Cálculo das resistências de cisalhamento
A norma especifica no item 17.4.2.1 que devem ser verificadas simultaneamente duas condições, para que a resistência do elemento estrutural seja considerada satisfatória, são elas:
Vsd ≤ Vrd2
Vsd ≤ Vrd3 = Vc + Vsw
Onde:
Vsd = força cortante solicitante de cálculo (Vk.ɣf);
Vrd2 = força cortante resistente de cálculo, referente à ruína das diagonais comprimidas de concreto (depende do ângulo θ);
Vrd3 = Vc + Vsw = força resistente de cálculo relativa à ruína por tração diagonal, onde Vc é a parcela resistida pelo concreto e Vsw é a parcela resistida pela armadura transversal, que também possui relação com o ângulo θ.
Modelo de Cálculo I – NBR 6118:2014
O modelo de cálculo I, expresso pelo item (17.4.2.2) da norma, admite o modelo de treliça clássico, onde o ângulo θ de inclinação das bielas de compressão (diagonais comprimidas) é fixado no valor de 45º. Além disso, o modelo admite ainda que a parcela complementar Vc tenha valor constante, independente de Vsd. Este modelo é o mais utilizado em projetos estruturais atualmente.
Na primeira etapa que é a verificação quanto à compressão diagonal do concreto, para o Modelo de cálculo I, temos que:
A segunda etapa consiste na determinação da armadura transversal:
Onde:
bw = menor largura da seção;
d = altura útil da seção (0,9.h);
Vc = Vc0 para flexão simples
Asw = área de aço da armadura transversal (estribos);
S = espaçamento entre os elementos de armadura transversal (estribos);
Fywd = tensão da armadura transversal passiva, fixado no valor de 4350 Kgf/cm².
Modelo de Cálculo II – NBR 6118:2014
O modelo de cálculo II é expresso pelo item 17.4.2.3 da norma. Este admite a analogia de treliça generalizada, onde o ângulo θ de inclinação das bielas de compressão (diagonais comprimidas) varia livremente entre 30º e 45º. Admite ainda que a parcela complementar Vc sofra redução com o aumento de Vsd.
Com isso, na verificação da compressão diagonal do concreto, temos que:
Na determinação da armadura transversal:
Vrd3 = Vc + Vsw
Para flexão simples, temos que:
É importante ressaltar que tanto para o modelo de cálculo I como para o II deve ser realizada a verificação quanto aos espaçamentos máximos, seguindo as especificações do item 18.3.3.2 da norma:
Quanto ao espaçamento mínimo entre os estribos, no eixo longitudinal da peça, este deve ser suficiente para permitir a passagem do vibrador, a fim de garantir um bom adensamento do concreto.
Exercício de dimensionamento de vigas ao cisalhamento
Realizaremos aqui o dimensionamento das armaduras transversais de uma viga pelo Modelo de cálculo I da NBR 6118:2014. A viga possui as seguintes características:
Considerando:
Concreto C20
Aço CA-50
bw = 25 cm
h = 90 cm
d = 80 cm
Diagrama de esforço cortante da viga:
Com isso temos que a cortante máxima (Vk) = 171,9 KN = 17190 Kgf.
Verificação da diagonal comprimida do concreto
Assim, Vsd ≤ Vrd2, portanto OK!
Cálculo das armaduras
Vsd ≤ Vrd3
Vrd3 = Vc + Vsw
No cálculo do Vc, para obtermos o resultado em Kgf multiplicaremos o fctd por 10:
Considerando que para estabelecer a verificação da norma a parcela resistida pelo concreto mais a parcela resistida pela armadura tem que ser no mínimo igual a Vsd, então:
Isso quer dizer que a parcela da armadura deverá resistir a um esforço de 11003,49 Kgf. Para calcular essa parcela vamos adotar barras de Ø 6,3 mm, então:
Como o estribo é composto por 2 ramos, o Asw da barra que adotamos será multiplicado por 2 e utilizado em centímetros, além disso como o aço que estamos utilizando é um CA-50, o Fywd será limitado a 4350 Kgf/cm², então:
Verificação do espaçamento máximo segundo o item 18.3.3.2 da NBR 6118:2014:
Vsd = 24066 Kgf
0,67.Vrd2 = 0,67.70971,43 = 47550,86 Kgf, portanto:
S calculado = 17 cm, portanto Ok! Então: Ø 6,3 mm c/ 17cm.
Cálculo da armadura mínima
Em alguns trechos da viga, a intensidade da força cortante é bem menor que a máxima para qual foi calculada os estribos no passo anterior, por isso devemos calcular a armadura mínima para ser utilizada nesses trechos:
Para o cálculo do espaçamento da armadura mínima, iremos adotar barras de Ø 6,3 mm.
α = é a inclinação dos estribos em relação ao eixo longitudinal do elemento estrutural, então:
Verificação do espaçamento máximo segundo o item 18.3.3.2 da NBR 6118:2014:
S calculado = 24 cm, portanto Ok! Então: Ø 6,3 mm c/ 24cm.
Nessa etapa iremos calcular até quanto de esforço cortante a armadura mínima calculada no item anterior pode resistir:
Desta forma, podemos utilizar até 15 tf de esforço cortante com a armadura mínima (Ø 6,3 c/ 24 cm) e posterior a isso (Ø 6,3 c/ 17 cm) para combater os esforços de cisalhamento.
Finalizando
Neste artigo vimos a importância do correto dimensionamento de vigas de concreto armado ao cisalhamento, entendemos a analogia do modelo de treliça utilizado nos dimensionamentos, vimos também como funcionam os modelos de cálculo propostos pela norma e, por fim, realizamos um dimensionamento completo dos estribos de uma viga de concreto armado.
Caso tenha interesse em acompanhar meus conteúdos acerca da engenharia de estruturas, acesse meu canal clicando aqui!
Espero ter contribuído para o seu conhecimento! Deixe nos comentários sua percepção sobre o assunto.
Até a próxima!