Neste artigo vamos avaliar como determinar a altura do Bulbo de Tensões em Radier. A forma de determinar a altura do bulbo de tensão em uma fundação do tipo Radier é encontrada na página 129 do livro de Fundações – Volume Completo dos Professores Velloso e Lopes (2011).
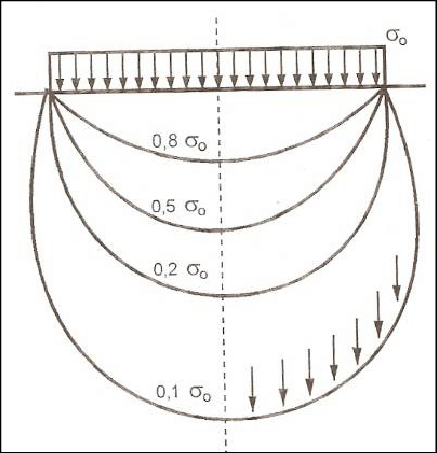
Onde: “Por outro lado, há uma questão controvertida: no caso de radiers, deve-se usar na correção o B do radier (muito grande, causando um kv pequeno). Se as cargas forem concentradas e muito espaçadas (l>2,5R), pode-se usar, na correção da dimensão, em vez de B, uma largura de influência de 2R (ver Fig. 6.10), sendo (ver item 9.2.4):
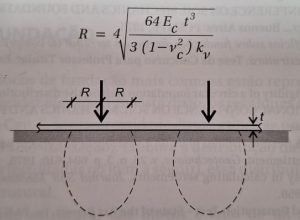
Em que as variáveis são:
Ec=Módulo de Young do material da placa (concreto, p:ex);
t= Espessura da placa
vc= Coeficiente de Poisson do material da placa (concreto, p:ex);
kv= coeficiente de recalque vertical
Podemos utilizar um exemplo prático – Bulbo de Tensão em Radier:
Em primeiro lugar, imagina-se um Radier de 16cm de espessura com fck de 25MPa.
Ec= 240.000 kgf/cm²
t= 16cm
vc= 0,2
Definição do coeficiente de recalque vertical
Então, para determinar o valor de kv necessitamos de correlações, uma das mais utilizadas é a tabela de Terzagui de 1955.
Pensando em um exemplo hipotético mais abrangente, ou seja um solo argiloso muito rijo ou uma areia medianamente compacta, podemos adotar como valor inicial de ks1 como:
ks1=4kgf/cm³
Ainda do livro dos professores Velloso e Lopes (Volume Completo, 2011):
“Segundo o American Concrete Institute (1988), a passagem do ks1, obtido no ensaio de placa , para o kv, a ser utilizado no cálculo da fundação, pode ser feita com:”
kv=ks1\left ( \frac{b}{B} \right )^{^{n}}
b= dimensão da placa (no caso da tabela de Terzagui 1pé ou 30,48cm);
B= menor dimensão ou diâmetro da fundação;
E sobre a variável b, Velloso e Lopes seguem:
“onde n varia entre 0,5 e 0,7. Se a espessura da camada compreensível abaixo da fundação for menor que 4B, deve-se adotar o menor valor de n.”
Na prática, para definir o valor de n, devemos avaliar a espessura de solo entre o fundo da fundação e o topo rochoso (camada compressível). Se a espessura de solo for menor que 4B, devemos adotar n=0,5, caso contrário, n=0,7.
Adotaremos para o nosso exemplo B=200cm a princípio e ratificaremos a posterior.
Ainda para fins de exemplo, utilizaremos valor de n=0,7 imaginando horizonte de camada compressível maior que 4B, de tal forma que:
kv=4\left ( \frac{30,48}{200} \right )^{^{0,7}}
kv=1,072kgf/cm³
Vamos partir de um valor estimado de coeficiente de recalque vertical e posteriormente realizaremos o ajuste, de forma reiterada até encontrarmos o valor correto.
Assim:
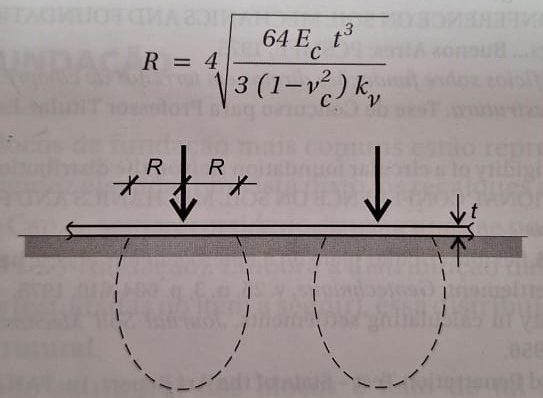
R=\sqrt[4]{\frac{64\times Ec\times t^{3}}{3\left ( 1-\nu c^{^{2}}\right )\times kv}}
R=\sqrt[4]{\frac{64\times 240.000\times 16^{3}}{3\left ( 1-0,2^{^{2}}\right )\times 1,072}}
R=377,82cm
B=755,65cm
D=2\times B
D=2\times 755,65 = 1511,30cm=15,11m
Iterações:
Realizando uma segundo iteração agora com B=755,65cm:
kv=4\left ( \frac{30,48}{755,65} \right )^{^{0,7}}
kv=0,423kgf/cm³
Assim:
R=\sqrt[4]{\frac{64\times Ec\times t^{3}}{3\left ( 1-\nu c^{^{2}}\right )\times kv}}
R=\sqrt[4]{\frac{64\times 240.000\times 16^{3}}{3\left ( 1-0,2^{^{2}}\right )\times 0,423}}
R=476,71cm
B=953,42cm
D=2\times B
D=2\times 953,42 = 1906cm=19,06m
Realizaremos uma terceira iteração buscando a convergência, agora com B=953,42cm:
kv=4\left ( \frac{30,48}{953,42} \right )^{^{0,7}}
kv=0,359kgf/cm³
Assim:
R=\sqrt[4]{\frac{64\times Ec\times t^{3}}{3\left ( 1-\nu c^{^{2}}\right )\times kv}}
R=\sqrt[4]{\frac{64\times 240.000\times 16^{3}}{3\left ( 1-0,2^{^{2}}\right )\times 0,359}}
R=496,67cm
B=993,33cm
D=2\times B
D=2\times 953,42 = 1987cm=19,87m
Apenas uma quarta, estamos próximos da convergência, agora com B=993,33cm:
kv=4\left ( \frac{30,48}{993,33} \right )^{^{0,7}}
kv=0,349kgf/cm³
Assim:
R=\sqrt[4]{\frac{64\times Ec\times t^{3}}{3\left ( 1-\nu c^{^{2}}\right )\times kv}}
R=\sqrt[4]{\frac{64\times 240.000\times 16^{3}}{3\left ( 1-0,2^{^{2}}\right )\times 0,349}}
R=500,18cm
B=1000,37cm
D=2\times B
D=2\times 1000,37 = 2000,75cm=20,01m
Desta forma chegamos a um resultado que apresenta uma convergência aceitável, com resultado aproximado de 20m de altura de bulbo de tensão.
Verificação em Elementos Finitos – Bulbo de Tensão em Radier:
Com a finalidade de validar-se nossos cálculos manuais, realizaremos a modelagem do mesmo Radier em software de elementos finitos – SAP 2000 e compararemos os resultados com o obtido pelas formulações.
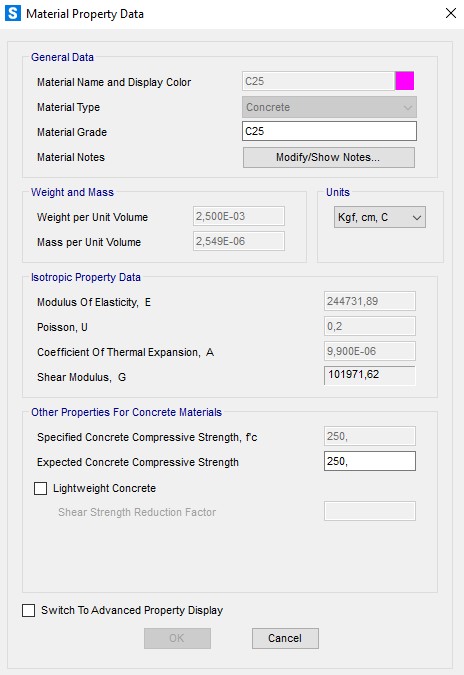
O material da placa foi modelado com as seguintes características:
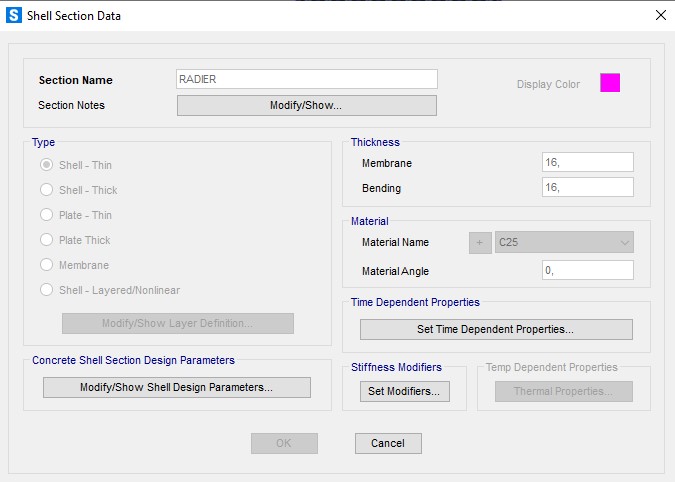
Já a placa foi modelada com as seguintes características:
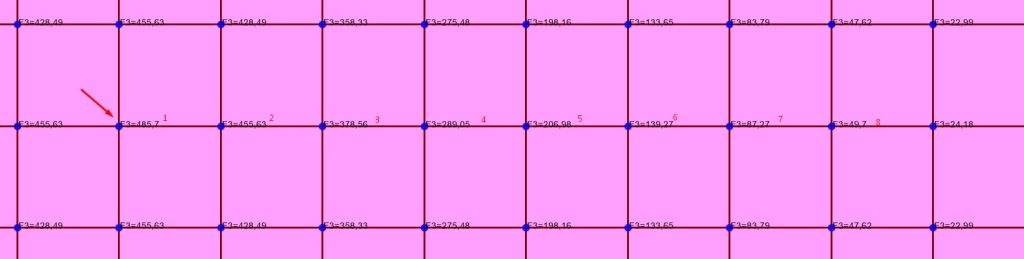
Em primeiro lugar, as molas foram aplicadas ao modelo imaginando inicialmente o kv=1,072kgf/cm³, como aplicaremos no nó, precisamos multiplicar por sua área de influência. Foi modelado uma malha de 38×38 com distância entre nós de 48,65cm, totalizando uma placa de 18x18m, conforme pode ser visto na imagem abaixo:
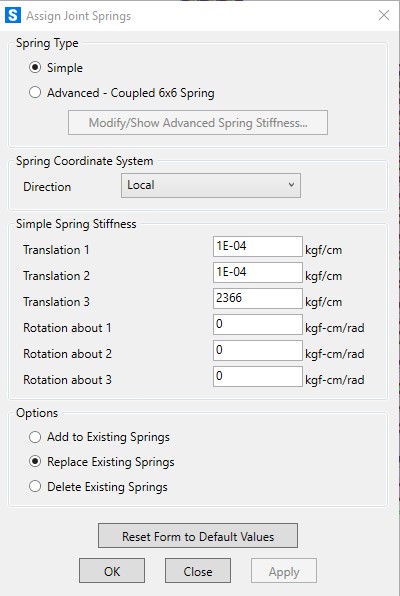
Aplica-se então a cada nó uma mole vertical de 1*48,65*48,68=2366,823kgf/cm:
Aplica-se então ao modelo uma carga de 30 tonelada força no centro da placa, distribuída em 4 nós.
A análise foi realizada excluindo o peso da placa, que para a análise proposta não tem influência. As deformações obtidas foram as seguintes:
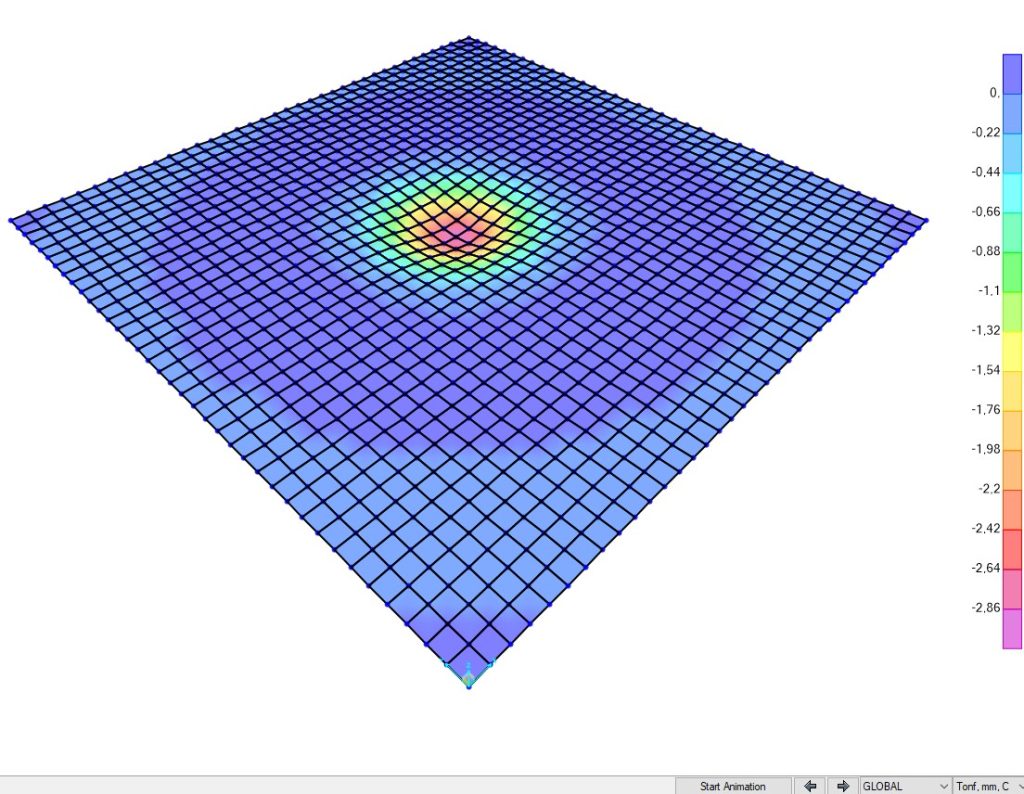
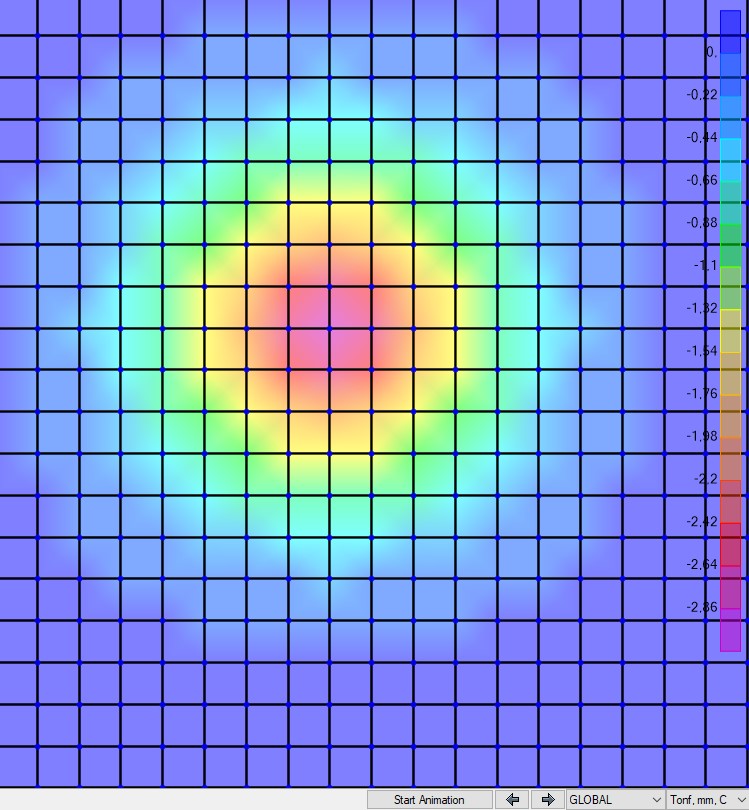
Assim, a resultante nos nós foram as seguintes:
Critério para avaliação do Bulbo de Tensão em Radier:
Em suma, utilizou-se como critério a premissa de que o raio se estende até 5% da carga máxima de reação no nó mais próximo ao centro percebemos:
Nó mais carregado=716,18kgf
5% de 716,18kgf = 36kgf
Ou seja no Bulbo de Tensões em Radier, se estende por 7 segmentos de reta, resultando em um raio de 7 x 48,65 = 340,55cm
B=2xR=2×340,55=681,10cm
Assim sendo, realiza-se uma segunda iteração buscando a convergência, agora com B=681,10cm:
kv=4\left ( \frac{30,48}{681,10} \right )^{^{0,7}}
kv=0,455kgf/cm³
Assim, a mola que deve ser aplicada a cada nó é de 0,455*48,65*48,68=1076,90kgf/cm
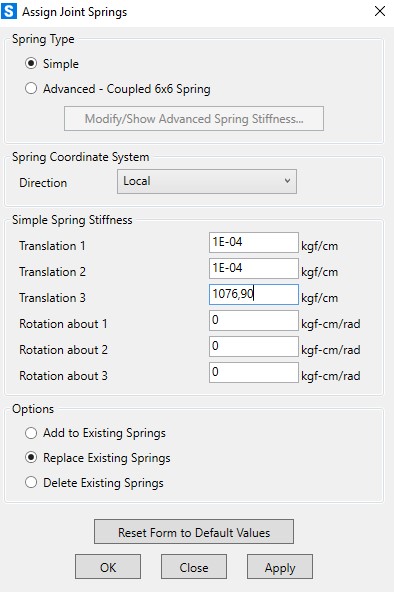
Assim, a resultante nos nós foram as seguintes:
Utilizando como critério a premissa de que o raio se estende até 5% da carga máxima de reação no nó mais próximo ao centro percebemos:
Nó mais carregado=506,7kgf
5% de 716,18kgf = 25,33kgf
Por conseqüência, o Bulbo de Tensões em Radier se estende por 8 segmentos de reta, resultando em um raio de 8 x 48,65 = 389,20cm
B=2xR=2×389,20=778,40cm
Realizaremos uma segunda iteração buscando a convergência, agora com B=778,40cm:
kv=4\left ( \frac{30,48}{778,40} \right )^{^{0,7}}
kv=0,414kgf/cm³
Assim, a mola que deve ser aplicada a cada nó é de 0,414*48,65*48,68=979,930kgf/cm
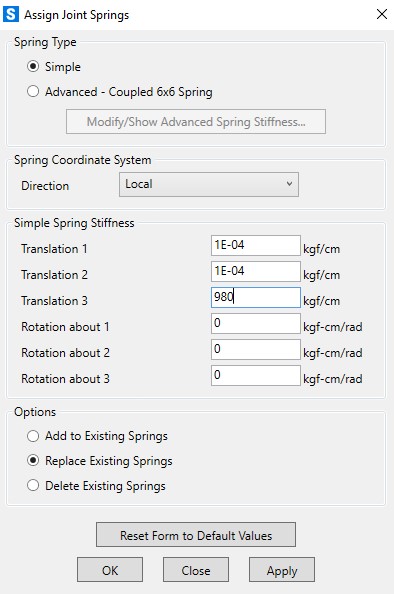
Já a resultante nos nós foram as seguintes:
Convergindo, para o mesmo resultado da iteração anterior, 8 segmentos.
Portanto, os resultados obtidos através da modelagem de elementos finitos e Winkler:
R= 8 x 48,65 = 389,20cm
B=2xR=2×389,20=778,40cm
Portanto a altura do Bulbo de Tensões em Radier
A=2×778,40=1556,80cm=15,57m
Isso resulta em uma divergência de 22,15% na altura do Bulbo de Tensões em Radier, em relação ao cálculo manual, onde o resultado da altura do bulbo de tensão foi de 20m.
Conclusão – Bulbo de Tensão em Radier:
Em conclusão, não me parece, em primeira análise, uma grande diferença tendo em vista as incertezas geotécnicas e estruturais envolvidas.
Além do mais, percebemos o Radier como elemento de fundações que trabalha justamente conforme a sua função, ou seja, função de distribuir as cargas vindas da estrutura em uma área maior.
Ora, se isso é verdade, não há que se duvidar que as sobrecargas realizadas por elementos do tipo Radier vão a profundidades maiores do que elementos de fundação do tipo Sapata.
Porém, existe sim uma grande mudança, trata-se da magnitude da sobrecarga realizada pelo bulbo de tensão do Radier.
Enquanto em elementos isolados por vezes distribuímos ao solo tensões que chegam de 4 a 6 kgf/cm³ dependendo do solo, no Radier percebemos uma sobrecarga muito menor devido a área de contato ser muito maior.
Só para ilustrar, veja o exemplo de cálculo que realizamos onde distribuímos uma carga de 30.000kgf, carga que pode ser comparada a carga de pilar bastante carregado de um sobrado.
O nó mais carregado do Radier estudado ficou com 485,7kgf que distribui em uma área de influência de 48,65×48,65=2.366,82cm², desta forma a tensão máxima aplicada ao solo é de 485,7/2366,82=0,2kgf/cm².
Agora imagine essa mesma carga de 30.000kgf em uma sapata de 100x100cm = 30.000/10.000= 3kgf/cm², bastante diferente né?
Praticamente 10x menos carga será aplicada no solo no caso do Radier.
Apesar disso, essas cargas no Radier tendem a percorrer até horizontes de solo mais profundos. Talvez isso não seja um problema, tendo em vista que a região mais carregada é de 0,2kgf/cm², imagina o final do bulbo de tensão onde as cargas são de 10% da carga máxima. Teríamos uma carga aplicada de 10% de 0,2kgf/cm² ou seja uma tensão solicitante de 0,02kgf/cm², um valor praticamente nulo.
